全球清洁能源转型对关键矿产的需求正以前所未有的速度增长，而矿物加工环节却面临着两大核心挑战：

• 原料品位持续下降
• 过程动态极其复杂

原料组成和矿物学特性时刻波动，过程机理又难以精确建模，导致大量有用矿物随尾矿流失，既造成经济损失，也增加环境压力。

传统选矿厂主要依赖过程控制来稳定生产，PID控制器仍是主流，模型预测控制（MPC）被视为“先进”手段。但这些方法本质上是“先稳定、再优化”，在高度不确定环境下往往力不从心。

---

斯坦福大学研究团队提出了一种全新思路：将矿物加工明确建模为“不确定性下的优化问题”，核心框架正是 部分可观测马尔可夫决策过程（POMDP）。

他们以一个简化的浮选池为例，展示了如何通过 “信念更新” 同时实现信息采集与决策优化，在模拟实验中显著优于传统确定性方法。

本文将系统梳理这一技术路径，重点讲清楚POMDP的核心算法逻辑。

---

一、传统控制范式的瓶颈

矿物加工的不确定性主要来自两个维度：

• 状态不确定性（State Uncertainty）
  原料组成、粒度、矿物解离度等实时波动，难以全程精确测量。

• 模型不确定性（Model Uncertainty）
  对浮选动力学、水力学、表面化学等机理的认知存在偏差，任何机理模型都只是“近似”。

PID控制只能处理单变量或简单多变量系统，对非线性、强耦合的浮选回路效果有限。MPC虽然引入预测模型，但高度依赖准确的确定性模型。一旦模型失配或原料剧烈波动，性能就会显著下降。

选矿优化不能仅停留在“稳定运行”，而应直接以经济目标（如净现值NPV）为导向，在不确定性中主动决策。

---

二、POMDP：从“控制”转向“序贯决策优化”

POMDP（Partially Observable Markov Decision Process） 是处理不确定性环境下序贯决策的标准框架。

它与传统控制的最大区别在于：不假设能完全知道系统真实状态，而是通过“信念”来表达不确定性。

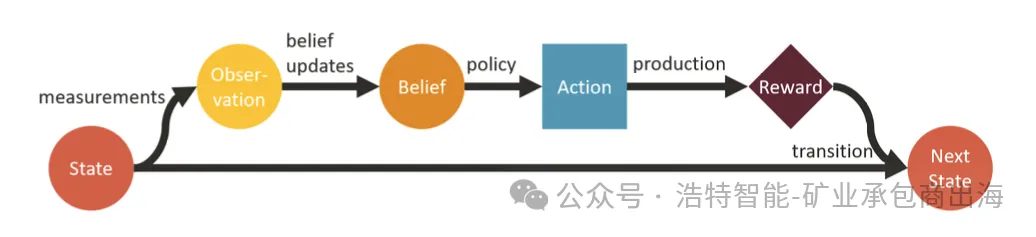
图1：POMDP关键组件的简化示意图，以及这些组件在每个时间步的演进过程。

POMDP七元组定义

⟨S, A, O, T, R, Z, γ⟩

• S：真实状态空间（原料组成、过程动态等，无法完全观测）
• A：动作空间（控制参数 + 是否测量）
• O：观测空间（传感器数据）
• T：状态转移函数
• R：奖励函数（经济目标，如NPV）
• Z：观测函数
• γ：折扣因子

核心机制：智能体根据当前信念（belief）——即对真实状态的概率分布——选择动作，获得奖励和新观测，然后更新信念。

信念更新的核心创新

研究团队采用 高斯过程（Gaussian Process） 分别建模两类不确定性：

• 原料组成的时序波动（状态不确定性）
• 机理模型与真实品位/回收率之间的系统性误差（模型不确定性）

每获得一次新测量数据，高斯过程就会进行顺序重拟合，信念均值曲线逐渐逼近真实值，不确定性区间（方差）同步缩小。

这让智能体真正做到“边采集信息、边优化决策”。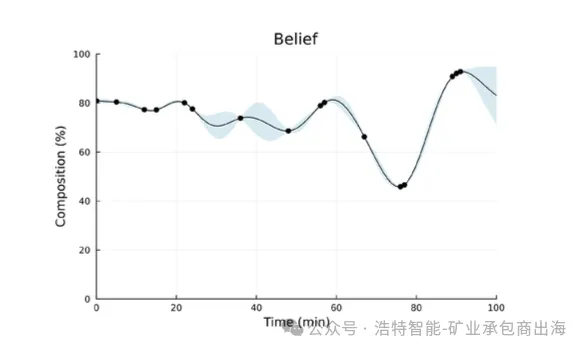图2：模拟结束时信念（belief）的一个示例。图中偶尔的测量值（黑点）用于更新信念及其相关不确定性（蓝色区域）。

求解算法：POMCP在线求解器

作者采用 POMCP（Partially Observable Monte Carlo Planning），基于 蒙特卡洛树搜索（MCTS） 实现。

该算法在每次决策时从当前信念采样大量未来轨迹，通过 Upper Confidence Bound（UCT） 策略快速探索最优动作，特别适合实时工业场景。

---

三、浮选池的POMDP完整建模

研究以批处理机械浮选池为例（便于实验室验证，后续可扩展为连续流程），参数大致参考磷酸盐浮选。

1. 状态（State）

• 原料组成 c（%）
• 精矿回收率 r（%）
• 精矿品位 g（%）
• 时间步 T

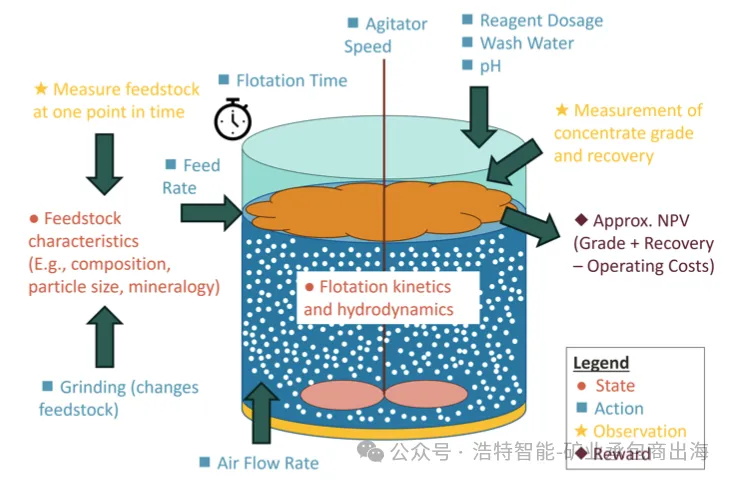
图3：浮选池的简单POMDP公式化表述。图中还包含了本文公式范围之外的其他可能的状态变量和控制参数，作为示例展示。

2. 动作（Action）

• 浮选时间 t（min）
• 空气流量 f（L/hr）
• 是否测量原料（可选动作）

3. 奖励函数（Reward）——直接以经济价值为目标

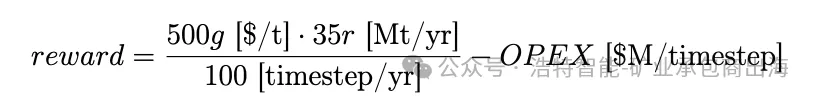
运营成本：

该奖励函数完美体现了品位-回收率-能耗三者的权衡。

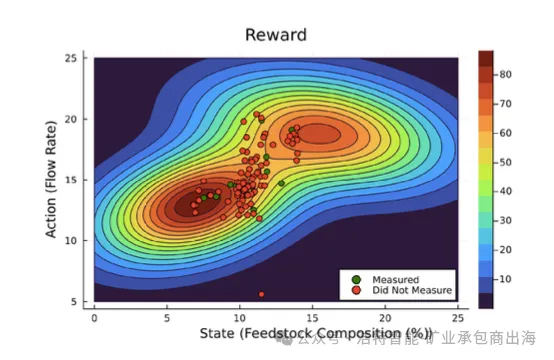
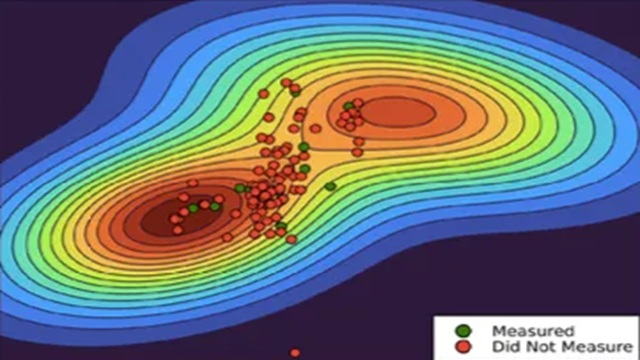
图4：奖励曲面示例（奖励作为状态和动作的函数），展示了智能体如何在进行测量所产生的成本与选择不良动作所产生的成本之间进行权衡。动作在状态随时间波动过程中持续执行，其中红色点表示未进行测量的时刻，绿色点表示已进行测量的时刻。

4. 初始机理模型（Prior）

回收率：

品位：

（k = 1 min⁻¹）

真实值 = 机理模型 + 随机误差（高斯过程）。智能体通过测量数据持续修正误差，实现从“不确定”到“越来越确定”的学习过程。

---

四、模拟实验验证：POMDP的显著优势

研究共进行100个时间步（模拟一年100批次），对比三种策略：

• PID控制器（基线）
• 模型预测控制（MPC）
• POMDP（POMCP求解）

主要发现

• 模型准确度高时：MPC略优于POMDP
• 模型不确定性增大时：POMDP优势迅速显现，低准确度场景下中位奖励显著更高
• 原料变异性越大：POMDP适应能力越强
• 原料未知（状态不确定性）时：POMDP随测量次数增加，性能提升速率明显快于MPC，并在一定阈值后全面超越

核心结论：在高不确定性环境下，POMDP通过主动学习和信念更新，更善于把有限信息转化为优化收益。

---

五、实际应用价值与前景

这一框架最大亮点在于：将信息采集与决策优化深度融合。

近期可落地场景

• 实验室浮选实验设计优化（可直接使用论文代码框架）
• 工业单槽浮选池运行优化（批处理 → 连续流程）

中长期扩展方向

• 整个浮选回路、全选矿厂的层次化POMDP建模
• 矿山-选厂一体化优化
• 关键矿产全供应链决策支持

无需额外硬件，只需现有传感器 + 计算资源即可部署。决策过程基于MCTS，具有一定可解释性，便于工程师理解和干预。

---

结语

矿物加工正在从“经验+控制”时代迈向“数据+智能决策”时代。

斯坦福这项工作提供了一个严谨的数学框架，证明在高度不确定性下，直接以优化为目标、用信念机制处理未知，比传统确定性控制更具鲁棒性。

对行业技术人员而言，理解POMDP的核心逻辑——
状态不可完全观测 → 信念表示不确定性 → 信念更新驱动学习 → 序贯优化 —— 将成为未来引入先进决策工具的重要起点。

我们期待更多选矿工程师与AI研究者共同推动这一方向的工业化落地。

---

参考文献
William Xu et al., AI-Driven Optimization under Uncertainty for Mineral Processing Operations, arXiv:2512.01977 (2025)

---

欢迎在评论区讨论：
你认为POMDP最有可能率先落地在哪个选矿环节？实验室还是工业现场？

END

X射线智能矿石分选机

HOT智能X射线分选机，是集X光、传感技术、电、气、磁于一体的高科技矿石分选设备，具有精准快速识别不同密度矿石的功能。自主研发全系列不同分辨率和不同能量谱段的 X 射线探测器，支持特殊定制和深度优化。